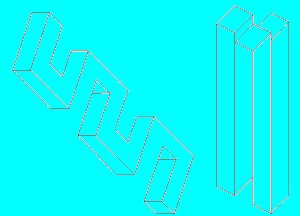|
|
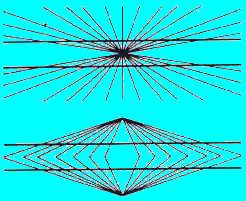
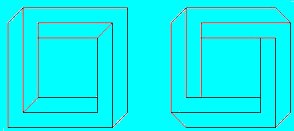
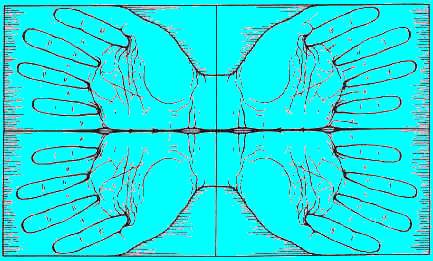
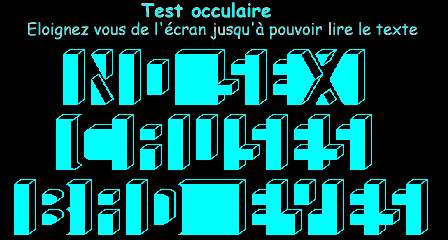
Les Illusions d'Optiques |
|
Attention !!! Si vous possédez ce genre d'illusion, J'en suis preneur.
N'hésitez pas à me les envoyer. Elles passerons elles aussi sur ce site.
Si vous ne pouvez toujours pas les voir, malgré les explications, essayez encore une fois ; plus tard !
|
Série 03 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Et pour finir
: |
|